
Simply speaking, significant digits are a way to indicate the precision of measured values, and the above rules enable you to preserve them in calculations. But an irrational number like \(\pi\), which is also a defined number, would require an infinite number of significant digits to exactly define, and if you use pi in a calculation, you should use enough significant digits so that it does not determine the number of significant digits in your answer. The advantage of using s to quote uncertainty in a.
Accurate standard deviation series#
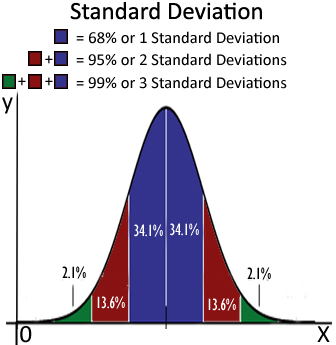
Twelve inches = 1 foot, there are no significant digits. The standard deviation, s, is a statistical measure of the precision for a series of repeated measurements. Now defined number may or may not have significant digits. The fact is, there is no uncertainty in an exact number, 3 cows is 3 cows. If one looks on the web one often sees people saying that a counted number has an infinite number of significant Figures, mathematically that may work, but it is incorrect, in that you do not need an infinite number of significant digits to exactly define a counted number. So it does not influence significant Figures. Quadratic approximations A simple, accurate formula to compute implied standard deviations can be. When a stock price is equal to a discounted strike price, this formula reduces to the Brenner-Subrahmanyam formula exactly. Significant Figures, Exact Numbers and Defined Numbers:Ī counted number is an integer and thus is an exact number, for which there is no uncertainty. yields accurate implied standard deviation values when stock prices deviate from discounted strike prices. Figure \(\PageIndex\): Normal Distribution curves for measurements made with different scales You can compensate for random error by making multiple measurements and averaging them. So to compensate for systematic error you need to recognize it, and adjust for it.

If you average the random error, you actually get a good estimate of where the bulls eye is. On the right the holes are scattered around the bulls eye in relatively equal directions, so the error is random. If you average all measurements that contain systematic error, you still miss the true value. This kind of error would occur if you use an old ruler to measure length, but the ruler was worn down over time so it was no longer twelve inches. The ones in the left image represents systematic error as all hits are to the left of the bulls eye. If the targets below represent attempts to hit the bulls eyes in an archery contest, they represent two types of error. Accuracy is how close your value or measurement is to the correct (true) value, and precision is how close repeated measurements are to each other. Step 4: Divide by the number of data points. Step 2: For each data point, find the square of its distance to the mean. What is the difference between random and systematic error? There are two concepts we need to understand in experimental error, accuracy and precision. Here's a quick preview of the steps we're about to follow: Step 1: Find the mean.


 0 kommentar(er)
0 kommentar(er)
